A Is Greater Than B

Prove: If $a < b$ , then $a < {\Large{{a + b} \over 2}} < b$ .

Before we start proving the theorem, allow'southward make sense of information technology beginning. What is the theorem trying to tell u.s. in plain English language? Let'southward break information technology down into something that we tin understand. Once more, here'south the theorem.

Suppose $a$ and $b$ are existent numbers, if $a < b$ then $a < {\Large{{{a + b} \over ii}}} < b$ .

If a is less than b then the average of a and b is between a and b.

The hypothesis of the theorem is $a<b$ , which suggests that $a \ne b$ . Since the two numbers are not equal to each other, information technology means that $a$ and $b$ are distinct and different numbers.

The interesting office is how we are going to use the hypothesis $a<b$ to arrive at the conclusion $a < {\Large{{{a + b} \over 2}}} < b$ .

If we just focus on the middle expression of the chemical compound inequality, the expression $\Large{{a + b} \over 2}$ is the average of the ii real numbers $\color{blue}a$ and $\color{red}b$ but $a \ne b$ .

Putting together what nosotros know now, the theorem is claiming that the boilerplate of two distinct numbers $\color{blueish}a$ and $\color{red}b$ is greater than $\colour{blueish}a$ (the smaller number) but less than $\colour{red}b$ (the larger number).

in the inequality a<(a+b)/2<b, a is the smaller number, (a+b)/2 is the average while b is the larger number

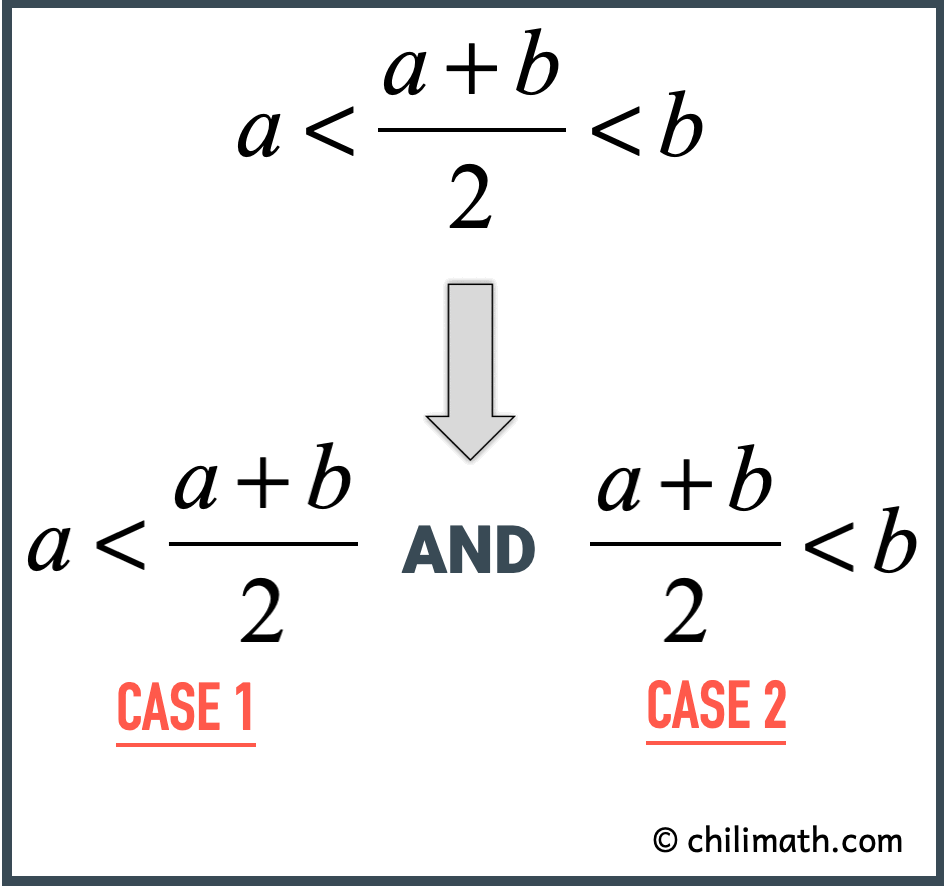
Since the conclusion is a compound inequality (conjunction), then we are going to prove two separate cases in order to prove the original theorem.

Case i: If $a<b$ , and so $a < {\Large{{{a + b} \over ii}}}$ .

Example ii: If $a<b$ , and so ${\Large{{{a + b} \over 2}}} < b$ .

Case 1 is when the average of a and b is greater than a. Case 2 is when the average of a and b is less than b.

Begin BEFORE WRITING THE PROOF

Note: The purpose of brainstorming in writing proof is for us to empathize what the theorem is trying to convey; and gather enough information to connect the dots, which will be used to bridge the hypothesis and the decision.

The side by side step is to strategize how we are going to prove the theorem by proving the ii cases using the Straight Proof Method.

Just first, let's exam out the theorem with bodily numbers and verify if indeed it is true.

Test i: Say $a=ii$ and $b=half dozen$ . Note, information technology is true that $a<b$ since $4<6$ .

Substitute the values of $a$ and $b$ then simplify.

$a < {\Big{{{a + b} \over two}}} < b$

$iv < {\Large{{{four + six} \over 2}}} < six$

$4 < {\Big{{{10} \over 2}}} < 6$

$four < 5< 6$ ✔︎

Test 2: Suppose $a=-three$ and $b=3$ . It is true since $a<b\,\,$ ⇨ $\,-3<3$ .

Plug in the values of $a$ and $b$ into the compound inequality and so simplify.

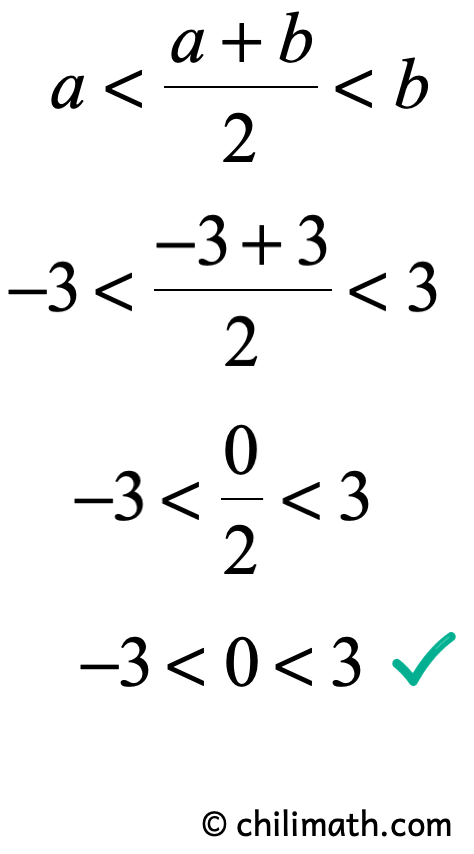
Nosotros will prove Case 1 and Case ii to prove the theorem. Below is the "big pic" again.

If a is less than b then a is less than the average of a and b. If a is less than b then the average of a and b is less than b.

SCRATCHWORK FOR CASE 1

Case one: If $a<b$ , and so $a < {\Large{{{a + b} \over two}}}$ .

For Case 1, the goal is to start with the hypothesis $a<b$ then perform some algebraic manipulations to get to the determination $a < {\Large{{{a + b} \over 2}}}$ .

It may not be obvious at first to show $a<b\,$ $\Big \to$ $\,a < {\Large{{{a + b} \over ii}}}$ . However, if we can piece of work information technology out backwards, such that nosotros begin with $\,a < {\Large{{{a + b} \over 2}}}$ and work towards $a<b$ , and so we might have only found a style to go from $a<b$ to $\,a < {\Large{{{a + b} \over 2}}}$ .

Side Calculation:

Start with $\,a < {\Large{{{a + b} \over 2}}}$ .
Multiply both sides of the inequality past $\color{reddish}ii$ to cancel out the denominator $ii$ on the right side of the inequality.
Subtract both sides of the inequality by $\color{carmine}a$ .
Voila! We got what we wanted!

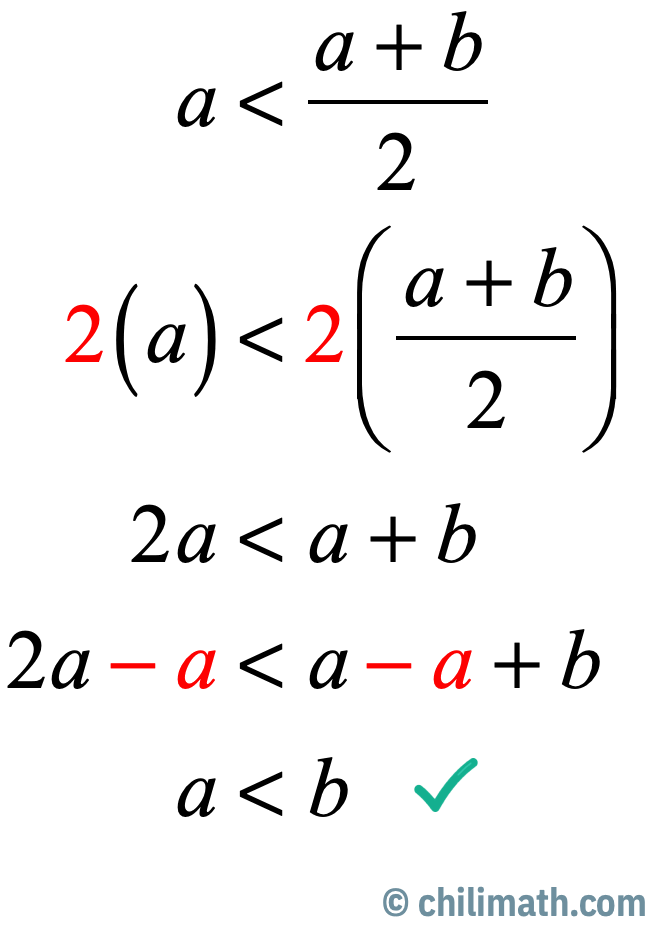
since 2a is less than the sum of a and b then a is less than b

Neat! Now, the only thing left that nosotros take to practise is to reverse the operations. This means we're going to add $\color{red}a$ on both sides of the inequality followed by dividing both sides by $\color{red}two$ .

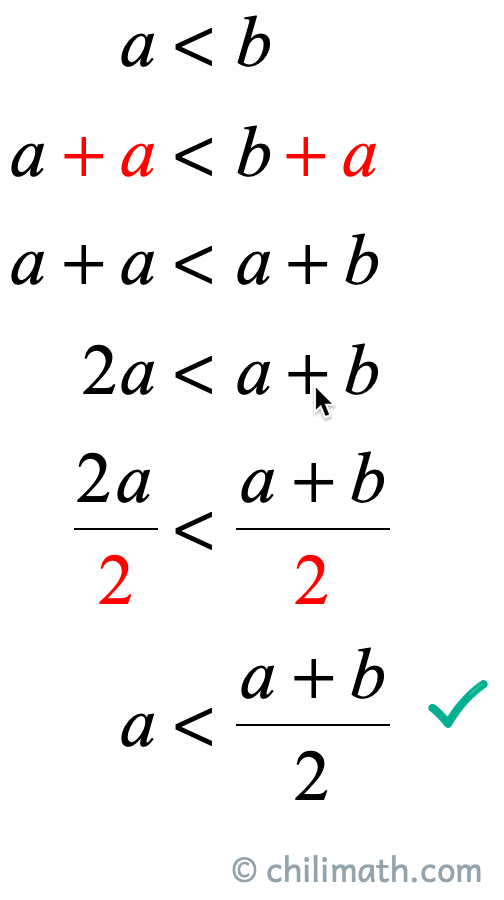
since twice a is less than the sum of a and b, it follows that a is less than the average of a and b.

Example 1 is now proved! Let's movement on to the next instance.

SCRATCHWORK FOR Instance 2

Example 2: If $a<b$ , then ${\Large{{{a + b} \over 2}}} < b$ .

For Case ii, we volition apply what we take learned from the scratchwork of Instance i. And then then, this time we are going to add $\color{red}b$ instead on both sides of the inequality and so equally divide both sides by $\color{red}2$ .

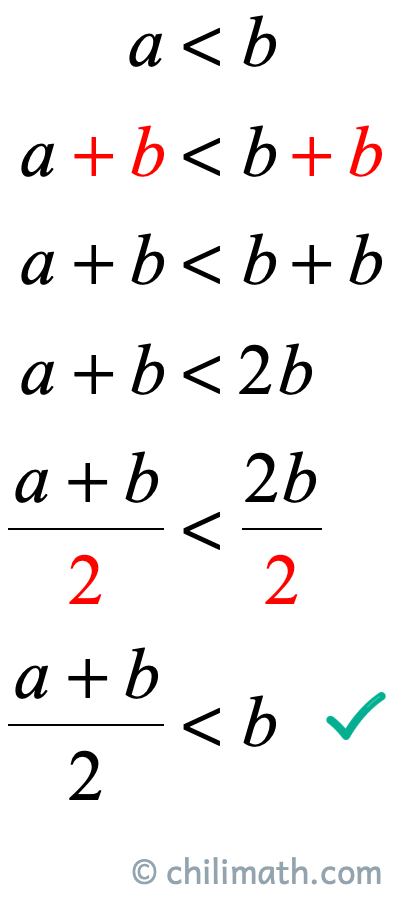
since the sum of a and b is less than twice b, then the average of a and b is less than b.

Example two is besides proved! Nosotros should at present be equipped with enough information to write the proof.

WRITE THE PROOF

THEOREM: Presume that $a,b \in \mathbb{R}$ , if $a < b$ then $a < {\Big{{{a + b} \over 2}}} < b$ .

PROOF: To show the provisional statement if $a < b$ and then $a < {\Large{{{a + b} \over 2}}} < b$ , we need to break information technology down into two cases. The showtime instance to prove: If $a<b$ , then $a < {\Large{{{a + b} \over two}}}$ . The 2nd case to evidence: If $a<b$ , and so ${\Big{{{a + b} \over 2}}} < b$ . Begin past proving Example one. Given that $a < b$ , nosotros add together $a$ on both sides of the inequality to get $a + a < a + b$ which tin can be simplified as $2a < a + b$ . Next, nosotros split up both sides of the inequality by $2$ to get $a < {\Large{{{a + b} \over ii}}}$ . Nosotros have only proved the outset case. For Case 2, given that $a < b$ , we add together $b$ on both sides to get $a < b \to a + b < b + b$ which is farther simplified every bit $a + b < 2b$ . Now divide both sides by $two$ to go ${\Large{{{a + b} \over 2}}} < b$ . We have just proved the second case. Since, nosotros have proved the two required cases, so nosotros accept proved the original theorem which is, if $a < b$ then $a < {\Large{{{a + b} \over two}}} < b$ .◼︎